Solved problems:

1: Single stage BJT amp (CE amp) designing (Dec 97 4 th sem)

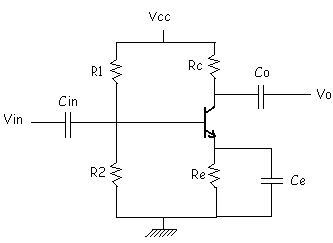
[Assume other required data]

 Circuit diagram

 Selection of Rc

mod(Av) = (hfe * RL')/(hie + (ðh * RL') )

Where  ðh = ((hie * hoe) - (hfe * hre))    [Get  hfe, hre, hie,hoe  from data sheet]

 ðh = 0.069

Hence

75 = (330 * Rc)/(4500 + (0.069 * Rc)

Hence

4.331 * Rc = 4500

Hence   Rc = 1039.02 ohm

We use HSV for better gain

Hence Rc = 1.2 Kohm

 Selection of operating point (Vceq, Icq)

Ic peak = Vo peak / RL'
Ic peak = 5.66/Rc = 4.714 mA
 

Icq = Ic peak + Ic min

 Assume Ic min = 0
Hence Icq = 4.714 mA

 Selection of Re

Re = Vre/Icq
Hence Re = 1/(4.714 * (10 ^ -3)) = 318 ohm

Select lower std value of Re so that voltage drop across Re is less which increases the voltage swing of o/p

Hence Re = 270ohm

 Selection of Vcc

Select higher std val

Hence Vcc = 18V

 Selection of R1 & R2

s = (1 + hfe max)/(1 + ((hfe max * Re )/(Rb + Re))

Hence 10 = 1 + 450)/(1 + ((450 * 270)/(Rb + 270))

Hence Rb = 2485.1 V

Vr2 = Vbe + Vre = 07 + (4.714 * 0.27) = 1.87 V
 

Vr1 = Vcc - Vr2 = 16.02 V

Assume Vbe = 0.6V

R1/R2 = Vr1/Vr2  .............(A)
[Get R1 in terms of R2 & substitute in Rb]

Hence R1 = 8.124 * R2

Rb = R1 parallel R2 = (R1 * R2)/(R1 + R2) = (8.124 * R2)/9.124 = 0.89 * R2

Hence 2.485.1 = 0.89 * R2

Hence R2 = 2790.99 ohm
Select lower standard value to make circuit indepent of beta

Hence R2 = 2.7 K ohm

Substitute in (A) to find R1

R1 = 8.124 * 2700 = 21934.8 K ohm
Select higher standard value so that circuit draws minimum current from supply

Hence R1 = 22 K ohm
 

 Selection of coupling capacitors

Selection of Ce:

Ce = 1/(2*pi * FL * Xce)  = 235.78 µ F

Hence Ce = 270 µ F | 50 V

Selection of  Cb:

Xcb = ((Rb) parallel (hie))

Cb = 1/(2 * pi * FL * Xcb) = 4.06 µ F

Hence Cb = 4.2 µ F | 50 V

Selection of Cc:

Xcc = Rc + RL    [If RL[load resistance] is not specified thenassume amplifier is connected to a similar next stage. Hence                                     RL = (Rb)parallel (hie)]

Cc = 1/(2 * pi * FL * Xcc) = 5.3 µ F

Hence Cc = 5.6 µ F | 50 V

[Draw the figure with designed values. Do all this in 30 minutes (1.8 min per mark)]

Designing of 1 stage FET amp

1: Design for device parameter variations
2: Design for midpoint biasing
3: Design for Zero thermal drift
4: Graphical methord
 

[Do not write text included in square bracket  ]

Type 1:Design against device parameter variations

 Selection of biasing circuit

Selection of Idq

 Selection of Vgsq

Vgs = Vp *  (1 - sqrt(Id/Idss))

Vgs max = - 1.4 V, Vgs min = - 0.29 V,

Vgsq = (Vgs max + Vgs min)/2 = -0.845 V

 Selection of Rs

Hence Rs = 620 ohm

 Selection of Rd

Hence RL' = 2719 ohm

Assume RL = infinity

RL' = (rd) parallel (Rd)

Hence  Rd = 2.87 K ohm
Select higher standard value

Hence Rd = 3.3 K ohm
 

 Selection of Vdsq

 Vo is given & Vdd is not given

 Selection of Vdd

 Selection of R1 & R2

Also
Vg = Vdd * R2/(R1 + R2)
Hence R1 = 0.47 * R2..................(A)

Assume R2 = 1 M ohm

Substitute in (A)

Hence R1 = 470 Kohm

Step 9: Selection of coupling capacitors

Selection of Cg:

Xcg = (R1) parallel (R2) = 319.72 ohm
Cg = 1/(2 * pi * FL * Xcg) = 0.0248 µ F

Select higher standard value
Hence Cg = 0.027 µ F | 25 V

Selection of Cd:

Cd = 0.0248  µ F

Select higher standard value

Hence Cd = 0.027 µ F | 25 V

Selection of Cs:

Select HSV
Hence Cs =  42 µ F | 25 V
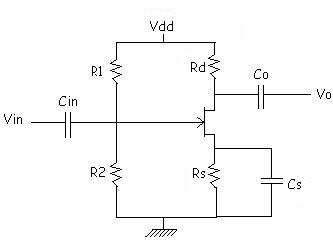
[Draw the figure with designed values]
 

Type 2: Design For midpoint biasing

 Selection of biasing circuit

[Draw the figure]

 

Selection of Idq

 Selection of Vgsq

Hence
Vgsq = Vp typ *  (1 - sqrt(Idq/Idss typ)) = 0.75 V
 

 Selection of Rs

Select HSV

Hence Rs = 220 ohm

 Selection of Rd

Gain of JFET amplifier, mod(Av) = gm * RL'

 RL is not given
Hence assume RL = infinity

RL' = (rd) parallel (Rd)
 Rd = 3.03 Kohm

Select HSV
Hence Rd = 3.3 ohm

 Selection of Vdsq

 Selection of Vdd

Hence Vdd = 20 V

 Selection of Rg

 Selection of coupling capacitors

Selection of Cg:

Select HSV

Hence Cg = 0.018 µF | 50 V

Selection of Cd:

Select HSV
Hence Cd = 0.01 µF | 50 V

Selection of Cs:

Select HSV
Hence Cg = 81 µF | 50 V
 

[Draw the circuit with designed values]

Type 3: Design for zero thermal drift (May 98)

 Selection of biasing circuit

We use self bias circuit
[Draw the figure]
 

 Selection of Vgsq

Hence Vgsq = -1.87 V

 Selection of Idq

 Selection of Rs

 Selection of Rd

Gain of JFET amplifier, mod(Av) = gm * RL'
 

 RL is not given
assume RL = infinity
RL' = (rd) parallel (Rd)

Hence Rd = 8.33 Kohm

 Select higher standard value
Hence Rd = 9.1 K ohm
 

Step 6: Selection of Vdsq

Step 7: Selection of Vdd

Step 8: Selection of Rg

Step 9: Selection of coupling capacitors

Selection of Cg:

Xcg = (Rg)
Cg = 1/(2 * pi * FL * Xcg) = 0.0079 µF

Select higher std value

Hence Cg = 0.01 µF | 25 V

Selection of Cd:

Hence Cd = 0.0079 µF

Select higher std val
Hence Cd = 0.01 µF | 25 V

Selection of Cs:

Select HSV

Hence Cg = 12 µF | 25 V
 

[Draw the circuit with designed values]

Graphical method

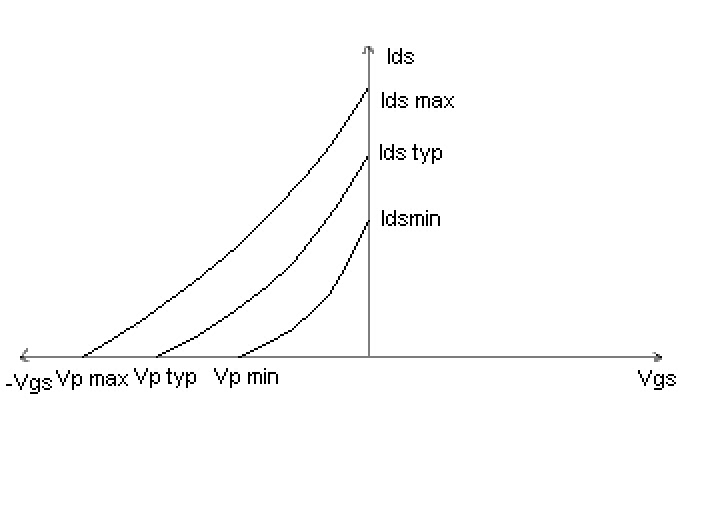
    [In graphical methord draw the graph of Ids against Vds [Values given in data sheet.You will be given the value/s of or range of Ids  (2 values(max or min) or range of values for device parameter variation & single value(typ) for other methods)]

    [Plot the required value/s of Vgs & find Vgsq & continue with the usual method. The answers in the 2 methods will differ a lot for the same problem. For device parameter variation use max & min curve to calculate Vgs max & min resp. For other methods use typ curve unless mentioned otherwise ]
 
 
 
 
 
 
 
 

Designing of 2 stage BJT amp

Av = Av1 * Av2

(Av1/Av2) = (Ro1/Ro2)

Assume (Ro1/R02) = 0.5

Hence Av2 = 2* Av1

Hence Av = 2 * ((Av1) ^ 2)

Hence 1000 = 2 * ((Av1) ^ 2)

Hence Av1 = 31.62

&Av2 = 63.24

We use BC 147A

Selection of Rc2:

63.24 = (220 * Rc2)/2700

Hence Rc2 = 776.18

Take higher std value

Hence Rc2 = 820 ohm

Selection of operating point :

Hence Vceq2 = 4.617 ohm
 
 

Icq2 = Ic2peak + Ic2min

Assume Ic2min = 0

Ic2 peak  = (Vopeak/Rc2) = 3.449 mA

Hence Icq2 = 3.449 mA

Seleciton of Re2

Hence Re2 = Vre2/Icq2

Hence Re2 = 289 ohm

Take LSV

Hence Re2 = 270 ohm

Selection of Vcc

Hence Vcc = 10.445 V

Take Vcc = 12 V

Selection of R3 & R4

Assume s = 8

Hence 8 = (1 + hfe)/(1 + ((hfe * Re2)/(Rb2 + Re2)))

[Substitute hfe, Re2 & find Rb2]

Hence Rb2 = 1971.13 ohm  [Do not standardise]
 
 

VR4 = Vbe + (Icq2 * Re2)

Hence VR4 = 1.63 V
 
 

VR3 = Vcc - VR4

Hence VR3 = 10.368 V
 
 

(VR3/VR4) = (R3/R4)

Hence (R3/R4) = 6.356

Now Rb2 = 1971.13 = (R3 * R4)/(R3 + R4)  = (6.356 * R4)/7.356

Hence R4 = Rb/0.864 = 2281.22 ohm

Take lower standard value

Hence R4 = 2.2 Kohm

Hence R3 = 6.642 * R4 = 13917.2 ohm

Select higher standard value

Hence R3 = 15 K ohm
 
 

Design of stage 1

Selection of Rc1

Av1 = 2000/Av2 = 29.93

 | Av1 | = (hfe typ * RL1)/hie

Hence RL1 = (Rc1) parallel (Zin2)

Where Zin2 = (R3) parallel (R4) parallel (hie) = 1121.6 ohm

 Hence Rc1 = 546.21 ohm

Taking higher std value

Hence Rc1 = 560 ohm

Selection of operating point

Let Vceq1 = Vceq2 = 4.617 V
       Vrc1 = Vrc2 = 2.828 V
       Vre1 = Vre2 = 0.931 V
       Icq1 = Vrc1/Rc1 = 5.05 mA
       Re1 = Vre1/Icq1 = 184 ohm

 Selection of R1 & R2

R2 = R4 = 2.2 K ohm

Selection of coupling capacitors

Selection of Ce1:

Select higher standard value

Hence Ce1 = 120 µF

Selection of Ce2:

Taking higher standard value

Hence Ce2 = 62  µF

Selection of  Cb1:

Cb1 = 1/(2 * pi * FL * Xcb1) = 1.418 µF

Taking higher std value

Hence Cb1 = 1.5 µF

Selection of  Cb2:

Xcb2 = Rc1 + ((Rb2) parallel (hie))

Cb2 = 1/(2 * pi * FL * Xcb) = 4.261 µF

Taking higher std values

Hence Cb2 = 4.7 µF

Selection of Co:

Xco = Rc + RL

Co = 1/(2 * pi * FL * Xco) = 0.819 µF

Taking higher std value

HenceCo = 1 µF

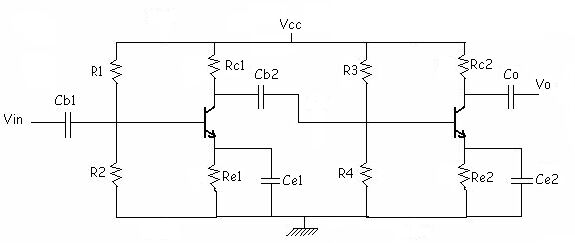
[Draw the figure with designed values. Do all this in about 36 - 40 minutes (1.8minper mark)]

Designing of power amps

Class A amplifier
Class B amplifier

Do not write text included in square bracket

Design of class A power amplifier

Selection of transistor

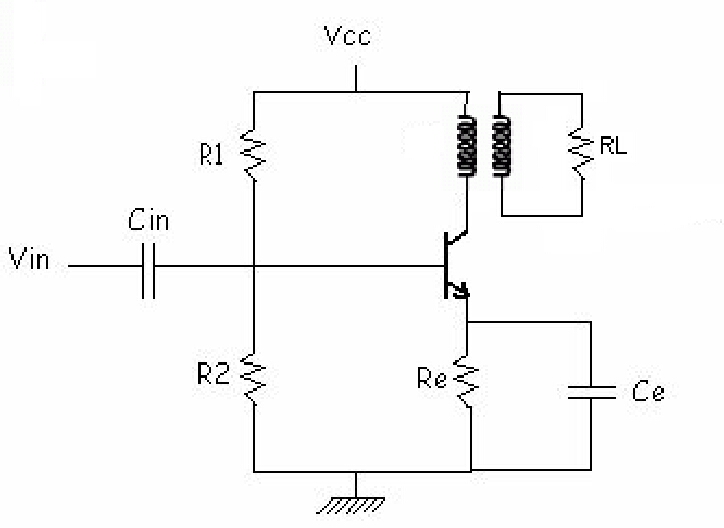
Power transmitted to load, PL' = PL/nt = 5.555W                  [nt = efficiency of transformer]
Assume  nT = 90% or 0.9

Q = (Pq max)/(PL') = 2
Hence Pq max = 11.111 W

Select transistor with Pd > 2 * Pq max
Select ECN 149 with Pd max = 30 W

 Selection of operating point

Vceq = Vcc - Vre = 10.8 V

Vce peak = Vceq - Vce sat = 9.8V

Ic peak = (2 * PL')/Vce peak = 1.134 A

Icq = Ic peak + Icmin
Assume Ic min = 0
Hence  Icq = 1.134 A

Step 3: Selection of Re & Ce

Pre = sqr(Vre)/Re = 1.44 W
Select Re = 1 ohm | 3 W

Ce = 1/(2 * pi * FL * RL) = 7957.74 µF

Since Ce is very high  we leave Re unbypassed

Step 4: Selection of R1 & R2

s = (1 + hfe max)/(1 + ((hfe max * Re )/(Rb + Re))

We have Rb = 9.89 ohm

Vr2 = Vbe + (Icq * Re) = 1.834 ohm
Vr1 = Vcc - Vr2 = 10.166 ohm
 

R1/R2 = Vr1/Vr2 = 5.543
Hence R1 = 5.543 * R2 .............(A)

Rb = R1 parallel R2 = (R1 * R2)/(R1 + R2) = (5.543 * R2)/6.543
Hence R2 = 11.67 ohm
Select lower standard value to make circuit indepent of beta
PR2 = ((VR2) ^ 2)/R2 = 0.336 W

Hence R2 = 10 ohm | 0.75 W

Substituting in (A) we get
R1 = 55.43 ohm

Select higher std value
Hence R1 = 56 ohm

PR1 = ((VR1) ^ 2)/R1 = 1.86 W

Select R1 = 56 ohm | 3.75 W

 Selection of  output transformer

RL' = (sqr(N1/N2)) * RL
Hence (N1/N2) = 1.697

Select audio frequency transformer with turns ratio 1: 1.697

 Calculation of  efficiency

 PL' FL = (Vce peak * Ic peak)/2 = 5.556 W

Pi dc = (Vcc * Icq) + (Vcc ^ 2)/(R1 + R2) = 15.79 W
Hence n FL = 0.3518 or 35.18 %

 For a class A amp max power dissipation occurs under no signal condition

Hence PD no signal = 30 W

Design of class B power amplifier (June 97)

Selection of transistor

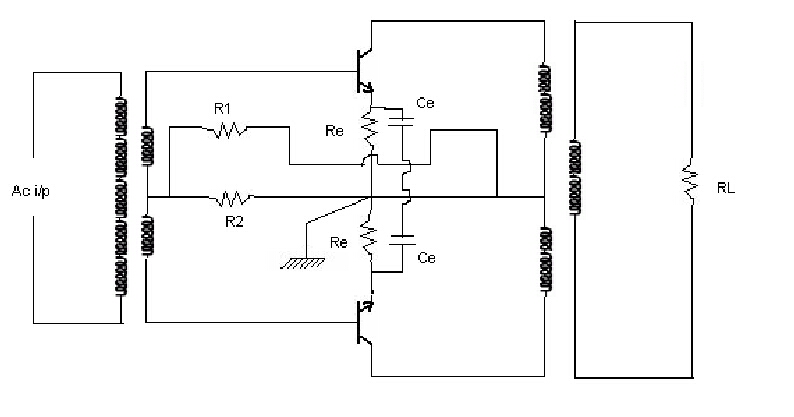
Q = (Pq max)/PL') = 1/5
PL = (I^2)/RL = 49/3 = 16.33W                                                                                                                                        PL' =PL/nT = 18.148 W

Hence Pqmax = 3.629 W

Select transistor with Pd > 2 * Pq max
Select transistor ECN 149 with Pdmax = 30W

 Selection of operating point

Vre = Vcc/10
Hence Vre = 2.5 V
 

Vceq = Vcc - Vre = 25 - 2.5
Hence Vceq = 22.5 V

Vce peak = Vceq - Vce sat  = 21.5 V

Ic peak = (2 * PL')/Vce peak = 2.519 A
Assume Ic min = 0

Icq = Icpeak + Icmin = 2.519A

Idc full wave = (2 * Idc peak)/pi = 0.967 A
Idc half wave = Idc peak/pi = 0.483 A

 Selection of Re & Ce

Pre = sqr(Vre)/Re = 1.225 W
Select Re = 5.1 ohm |3W
 
 

Ce = 1/(2 * pi * FL * RL)
Ce is too high hence leave Re unbypassed

 Selection of R1 & R2

s = (1 + hfe max)/(1 + ((hfe max * Re )/(Rb + Re))

Rb = 50.44 ohm             [Show the calculations]

Vr2 = Vbe + (Idc half wave * Re) = 3.163 V

Vr1 = Vcc - Vr2 = 21.83 V

  Assume Vbe = 0.6V

R1/R2 = Vr1/Vr2 = 6.903 .............(A)

Rb = R1 parallel R2 = (R1 * R2)/(R1 + R2)

Hence R2 = 57.747 ohm = 56 (LSV)

PR2 = (Vr1 ^ 2)/R1 = 0.178 W

Select lower standard value to make circuit indepent of beta
Hence R2 = 56 ohm | 0.5 W
 

Substitute in (A) to find R1                                                                                                                                                   R1 = 386.56 ohm

PR1 = 1.22 W

Select higher standard value so that circuit draws minimum current from supply
Hence  R1 = 390 ohm| 3 W

 Selection of  output transformer

RL' = (sqr(N1/N2)) * RL
Hence (N1/N2) = 2.172
Hence N1:N2 = 2.172 : 1
 

Power rating of primary  > PL'
ie power rating of primary > 18.148 ohm
 

Select audio frequency transformer with turns ratio 1:(N1/N2)
Select centre tap transformer with turns ratio 2.172 : 2.172 : 1 & power rating of 25 W

[Draw the circuit diagram with calculated values]
 
 

Top
Standard values